IMPORTANCIA DEL BLOG
Aquí estamos otra vez!!! Esta entrada va a ser cortita puesto que ,simplemente, les pondré un audio en el que expliqué la importancia que ha supuesto el blog para mí en estos 18 meses. Al fin podrán escuchar mi voz☺. Espero que les guste y felices vacaciones!!💃💜
TRIGONOMETRÍA
1. Razones trigonométricas.
2. Cómo calcular las razones de unos ángulos a partir de otros.
3. Ecuaciones trigonométricas.
4. Resolución de triángulos.
5. Reflexión
1. RAZONES TRIGONOMÉTRICAS.
Las razones trigonométricas de un ángulo α son las razones obtenidas entre los tres lados de un triángulo rectángulo. Es decir, la comparación por su cociente de sus tres lados a, b y c. Sea α uno de los ángulos agudos del triángulo rectángulo.
Aquí les dejo las fórmulas FUNDAMENTALES que deben saberse.
A continuación, voy a dejarles una sencilla tabla de las razones trigonométricas de los ángulos más comunes: 0º, 30º, 45º, 60º, 90º, 180º y 270º.

TRUCO: Podemos adivinar el seno de los ángulos 30º, 45º y 60º escribiendo en los numeradores la raíz cuadrada de los números 1, 2 y 3 y siempre con denominador 2. Sin embargo, para hallar el coseno tenemos que alterar el orden. Escribimos la raíz cuadrada de 3,2 y 1 y de denominador 2.
En el sistema sexagesimal de medida de ángulos, la unidad es el grado sexagesimal. Es decir, la 360 parte de un ángulo completo. Pero también hay otra unidad de medida de ángulos en el Sistema Internacional que es el radián.
Un ángulo completo = 360º = 2π rad
Un ángulo llano = 180º = π rad
Y si, por ejemplo, nos piden expresar en radianes un ángulo, tendremos que hacer una sencilla regla de tres. Multiplicar el ángulo por π y dividirlo entre 180º.
En el caso de que tengamos que pasar de radianes a grados sexagesimales, tendremos que multiplicar por 180 y dividir entre π.
SIGNO DE LAS RAZONES TRIGONOMÉTRICAS EN UNA CIRCUNSFERENCIA
Parece ser que algunos fallos que cometemos en los exámenes suelen ser por unos únicos signos que piensas que no tienen la menor importancia pero, en realidad, sí. Por ello, aquí les una imagen que deben de tener MUCHO OJITO 👀
2. ¿CÓMO CALCULAR LAS RAZONES DE UNOS ÁNGULOS A PARTIR DE OTROS?
Hay dos fórmulas fundamentales que te ayudarán a hallarlos.
Sen(a + b) = sen a * cos b + cos a * sen b
Cos(a + b) = cos a* cos b - sen a* sen b
Aunque sólo sean válidas para ángulos agudos, estas fórmulas sirven para cualquier ángulo. Simplemente tiene que reducirlo al primer cuadrante.
- Si está en el segundo cuadrante, tienes que restar 180º - x ángulo
- Si está en el tercer cuadrante, restar el ángulo menos 180º.
- Si está en el cuarto cuadrante, restarle 360º.
EJEMPLO: Calcular las razones trigonométricas de 75º.
Tenemos que tener en cuenta los ángulos comunes ya comentados anteriormente. Vemos como 75º es la suma de los ángulos 30º y 45º. Ahora, aplicando las fórmulas anteriormente dichas, podemos hallarlas.
Sen (30+45)= sen30 * cos45 + cos30* sen45
Sen 75= (1/2 )* (r.c. 2/2) + ( r.c. 3/2) * (r.c. 2/2)
Cos (30+45)= cos30* cos45 - sen30 * sen45
Cos 75= 1/2
tg 30 + tg 45
Tg 75= -------------------
1- (tg30 * tg45)
NOTA: Otro método para hallar la tangente es dividir el resultado de sen75 entre cos75.
3. ECUACIONES TRIGONOMÉTRICAS
Antes que nada, voy a escribirles algunos de los pequeños fallos que solemos cometer en trigonometría.
Así que por ello, les pondré unas fórmulitas que deberán de tener en cuenta si no quieren cometer este tipo de fallos.
Tg2a = sen2a/ cos2a
Sen^2x + cos^2x = 1
Sen2x= 2 senx * cos x
Cos2x= cos^2x - sen^2x
Sen 3x= sen (2x+x)
Sec^2a = 1+ tg^2a
En las ecuaciones trigonométricas intervienen funciones trigonométricas, que son periódicas, y por tanto, sus soluciones se pueden presentar en uno o en dos cuadrantes y además, se repiten en todas las vueltas.
Una ecuación trigonométrica es una ecuación en la que aparece una o más razones trigonométricas.
Para resolver una ecuación trigonométrica es conveniente expresar todos los términos de la ecuación con el mismo arco (ángulo) y después reducirlo a una razón trigonométrica, o bien, factorizar la ecuación si es posible. Veamos unos ejemplos.
Cos2a + 1= 4cosa
(Cos^2a - sen^2a) +1 = 4cosa
Cos^2a - sen^2a + 1- 4 cosa = 0
Cos^2a - (1- cos^2a) +1 - 4cosa = 0
Cos ^2a - 1 + cos^2a + 1 - 4cosa =0
Cos^2a + cos^2a - 4 cosa=0
2 cos^2a- 4 cosa= 0
2 cosa ( cosa- 2) =0
1era solución: cos a= 0 → a= 90º, 270 + n* 360 nEz
2da solución: cos a-2 = 0 → cosa= 2. NO TIENE SOLUCIÓN, puesto que ningún ángulo tiene un coseno mayor que 1.
También quiero comentar que estuvimos machacando mucho en clase el tema de demostrar identidades trigonométricas. Para ello tienes que recordar las fórmulas dichas anteriormente.
EJEMPLO:
4. RESOLUCIÓN DE TRIÁNGULOS.
El objetivo principal es calcular todos los lados y ángulos de un triángulo, para si poder hallar por ejemplo la altura de una torre.
Para resolver un triángulo, necesito:
- 2 lados y 1 ángulo comprendido
- 1 lado y 2 ángulos
- 3 lados
Mediante una fórmula conocidísima llamada " TEOREMA DEL SENO " podemos resolver un triángulo.
Aquí les dejo un ejemplo de un ejercicio de resolución de triángulos.
Aquí van unos enlaces de vídeos muy interesantes que explican adecuadamente el tema.
5. REFLEXIÓN
En mi opinión, la trigonometría es muy importante. Gracias a ella, hemos podido conocer la distancia del sol a la tierra, o también medir alturas o distancias.
Lo que más me cuesta es demostrar las identidades trigonométricas, puesto que hay veces que no sé cómo seguir desarrollando y me quedo pausada. Pero eso es cuestión de practicar para conseguir esa soltura que se necesita.
Lo importante de esta unidad simplemente es ser consciente de lo que está sucediendo en el día a día. Gracias a la trigonometría podemos saber cómo los albañiles construyen casas, cómo los capitanes de barco tienen en cuenta la medición de distancia entre puntos geográficos, etc.
Y con esta reflexión termino mi entrada de trigonometría... Nos vemos pronto!❤
TRABAJANDO CON TRIÁNGULOS
Aquí les enseño mi triángulo.
1. Para que haya un triángulo, si ladoB = 2 y ladoC = 1, ladoA debe ser como mínimo 1 y como máximo 3. Es decir, [1,3]
2. Para que se forme el triángulo, si ladoA=4 y ladoC= 1, ladoB debe ser como mínimo 3 y como máximo 5. Es decir, [3,5]
3. Para que se forme el triángulo, si ladoA=5 y ladoB=5, ladoC debe ser como mínimo 0 y como máximo 10. Es decir, [0,10]
NOTICIA MATEMÁTICA
Hola!! Hoy voy a hacer algo diferente. Voy a comentarles sobre un artículo que he leído acerca de cómo llamar la atención a estudiantes mediante unas... ¡Ecuaciones coloreadas! Así es, algo tan sencillo.
Kalid, un matemático, se topó con una vieja representación de una fórmula y le pareció una buena idea lo de las fórmulas coloreadas: asignar un color a cada término de una ecuación de modo que, luego, se puedan explicar en una frase (también coloreada) para que se entienda más facil. Aquí les enseño un ejemplo.
Vemos cómo de un solo vistazo se puede entender a qué se refiere cada término y de qué modo influye en la ecuación.
Desde mi punto de vista, me parece una buena idea, ya que te ayuda mucho a ver su estructura. Es verdad que el lenguaje matemático se inventó para evitar ambiguedades del lenguaje natural; pero, por ejemplo, a la hora de que la ecuación se empiece a poner más difícil (con paréntesis, corchetes, subíndices, etc.) muchas personas se van a la luna de Valencia porque empiezan a distorsionar la realidad. Por ello, este método me parece de lo más fabuloso.
Aunque no todo es tan bonito como te lo pintan (y nunca mejor dicho). También tiene algunas desventajas, como por ejemplo, las personas daltónicas no pueden aprovecharse de esto. O también, a la hora de imprimir apuntes, tendrás que imprimirlo en color.
En resumidas cuentas, a muchas personas les parecerá una bobada o muy infantil este método, y otras pensarán lo contrario. Pero esto es cuestión de uno mismo. Así que para gustos... ¡COLORES!
Url info: pinche aquí
Url info: pinche aquí
EXAMEN POR PAREJAS
Hola!! Hoy les voy a comentar sobre el examen que hemos hecho por parejas el día 30 de noviembre.
Lo he hecho con mi compañero Jhoel Vallejos. La verdad que pensábamos que estaba más o menos controlado, pero resultó ser que no. Faltó práctica por ambas partes.
Todo lo que salió en el examen lo habíamos dado en clase, pero de una forma más sencilla. Creo que el examen estuvo un poco más complejo pero es comprensible porque estábamos en parejas.
Nos dió tiempo de hacer el examen, aunque hubieron algunos que no los supimos hacer y otros que no los acabamos, pero no fue por falta de tiempo, sino falta de práctica.
Trabajar con Jhoel ha sido increíble, puesto que a pesar de que es nuevo en nuestro instituto y de no estar tan acostumbrado a nuestra manera de trabajar, ha sido capaz no tirar la toalla pese a las circunstancias (como muchos lo hubieran hecho) y seguir intentándolo hasta dar con la solución.
He reflexionado sobre una frase célebre que dice que a medida que vas creciendo, vas descubriendo que tienes dos manos; una para ayudarte a ti mismo y otra para ayudar a los demás.
NÚMEROS COMPLEJOS
ÍNDICE:
- Representación
- Triángulo de Pascal
- Potencias de i
- Formas de expresarlos y cómo pasar de una forma a otra
- Ejemplo de una operación
1. REPRESENTACIÓN

2. TRIÁNGULO DE PASCAL

3. POTENCIAS DE I

4. FORMAS DE EXPRESARLOS Y CÓMO PASAR DE UNA FORMA A OTRA

5. EJEMPLO DE UNA OPERACIÓN
REFLEXIÓN PERSONAL
Me ha costado mucho pillarle el truquillo a este tema, pero he estado practicando y la verdad que lo he llevado más o menos bien. Lo que más me ha costado ha sido cómo pasar de una forma a otra (sobre todo de la forma polar a forma binómica), puesto que tenía que tener en cuenta distintas fórmulas y recordar trigonometría del año pasado.
Realmente nos sirve para representar situaciones de la realidad cuya descripción y tratamiento es posible gracias a las propiedades de estos números.
NÚMEROS REALES
ÍNDICE:
- Redondeo
- Logaritmos
- Radicales
- Notación Científica
- Conjuntos
1. REDONDEO
Redondeo es el proceso mediante el cual se eliminan decimales poco significativos a un número decimal. Las reglas del redondeo se aplican al decimal situado en la siguiente posición al número de decimales que se quiere transformar; es decir, si tenemos un número de 3 decimales y queremos redondear a 2, se aplicarán las reglas de redondeo:
Si el dígito es menor que 5: Si el siguiente decimal es menor que 5, el anterior no se modifica.
Ejemplo: 12,612. Redondeando a las centécimas, debemos tener en cuenta el tercer decimal: 12,612= 12,61.
Si el dígito es mayor que 5: Si el siguiente decimal es mayor o igual que 5, el anterior se incrementa en una unidad.
Ejemplo: 12,618. Redondeando a 2 decimales deberemos tener en cuenta el tercer decimal: 12,618= 12,62.
2. LOGARITMOS
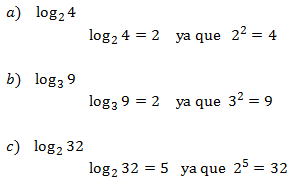
3.RADICALES

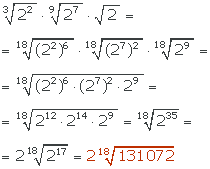
4. NOTACIÓN CIENTÍFICA

5.CONJUNTOS
REFLEXIÓN PERSONAL:
En mi opinión, todos los apartados que he dado hasta ahora tienen mucha importancia y no hay ninguna excepción. Tengo que matizar que los logaritmos los considero un poquito más sobresaliente que el resto puesto que es capaz de transformar un producto en una suma, un cociente en una resta, una potencia en una multiplicación sencilla y una raíz en una división sencilla.
La verdad es que he tenido muchas dificultades, sobre todo a la hora de radicalizar. debido a que me lío al cambiar de signo.
En general, yo creo que tiene mucho uso hoy en día y es conveniente saber dichos apartados para ser conscientes de lo que está pasando en nuestro alrededor y no dejarnos manipular por nadie.
La notación científica ,por ejemplo, la usamos muy a menudo cuando tenemos que hablar de cantidades muuuy pequeñas o muuuy grandes. Y con los demás apartados se me ocurren mínimos ejemplos, pero estoy convencida de que son muy útiles tanto en Matemáticas como en otras asignaturas que tengo.
Y con esta reflexión, finalizo mi entrada de números reales. ¡¡ESPERO QUE LES HAYA GUSTADO!! Nos vemos prontito
RESUMEN DE TODO EL CURSO
Para empezar, ha sido una idea muy maravillosa tener que escribir por ella blog, ya que tendrías tus apuntes guardados aquí y puedes mirarlos cuando quieras.
Hay personas que no se manejan muy bien con el ordenador/móvil, y eso puede llegar a ser una de las principales desventajas. Esto puede llegar a un desorden y tener todos tus apuntes alternados.
Para mí, es el primer año que uso este tipo de tecnología y realmente me ha agradado mucho, puesto que yo sí me manejo bien. Y espero que los próximos años sigamos con esto.
Gracias al blog, el curso me ha ido bien 😘
FUNCIONES A TROZOS
Hoy les escribo para enseñarles la imagen de un fantasma con funciones a trozos. He destacado en la zona de la cabeza y en una de sus mangas. Espero que les guste.
Color naranja: f(x) = -x^2 Si [-1.5 ≤ x ≤ 1.4]
Color azul: f(x)= 2.5(x-3.2)^2-4 Si [ 2 ≤ x ≤ 4.5]
FUNCIONES DE PROPORCIONALIDAD INVERSA
Hoy estoy de nuevo para enseñarles la imagen de una cantante (Rihanna) con funciones de proporcionalidad inversa. He querido destacarlo en las zonas de la cara y en su hombro derecho. Espero que les guste.
Color azul → f(x)= - (2/x-5,5)+ 2,15
Color verde → f(x)= - (0,2/x-0,1)+ 2
Breve explicación sobre este tipo de funciones:
Cuando las variables independiente y dependiente son inversamente proporcionales, es decir cuando aumenta la variable independiente, la variable dependiente disminuye en la misma proporción; y cuando disminuye la variable independiente,la variable dependiente aumenta en la misma proporción, entonces la función que las relaciona se dice que es de proporcionalidad inversa.
Las funciones de este tipo se representan: y = a/x , siendo 'a' un coeficiente. Por ejemplo: y= 2/x
Si el coeficiente fuera negativo, estaría por debajo del eje x.
Y esto es todo, espero que lo hayan entendido. Buen día.
PARÁBOLAS Y RECTAS
Como ya les he explicado dias atrás de cómo hacer una parábola, esta vez les explicaré de forma sencilla cómo realizar rectas sobre una imagen:
y = f (x-a) la función 'a' se desplaza a la derecha
y = f (x+a) la función 'a' se desplaza a la izquierda
y = f (x) + m la función se desplaza hacia arriba en la vertical OY
y = f (x) - m la función se desplaza hacia abajo en el eje OY
Y esto es todo, espero que lo hayan entendido. Feliz semana santa.
ÁLGEBRA
Bueno, hoy estoy aquí de nuevo para repasarles el tema de Álgebra y lo entiendan estupendamente, ya que queremos dejarlo definitivamente por acabado pero aprendido.
ÍNDICE:
- Monomios
- Polinomios (resolver operaciones, identidades notables, fracciones algebraicas, Ruffini y Teorema del Resto)
- Ecuaciones (primer y segundo grado, bicuadradas, raccionales e irracionales)
- Sistemas (problemas)
- Inecuaciones
1. MONOMIOS
Definición: Producto indicado de un número (coeficiente) por una o varias letras (parte literal) o bien un número solo.
Ejemplo:

Definición: Son aquellas expresiones enteras cuyas características (grado, coeficientes y variables) y por la forma como se presentan, guardan ciertas propiedades implícitas que las hacen notables.
Resolviendo operaciones:
→ IDENTIDADES NOTABLES
Definición: Las identidades notables son varias expresiones algebraicas que por su utilidad conviene conocer, ya que nos pueden ahorrar mucho tiempo en operaciones laboriosas
- Cuadrado de un binomio
- Suma por diferencia de dos monomios
→ FRACCIONES ALGEBRAICAS
→ REGLA DE RUFFINI
Definición: Esta regla es un método que nos permite dividir un polinomio entre un binomio y además permite localizar las raíces de un polinomio para factorizarlo en binomios. En otras palabras, posibilita dividir o descomponer un polinomio algebraico de grado n, en un binomio algebraico, y luego en otro polinomio algebraico de grado n-1.
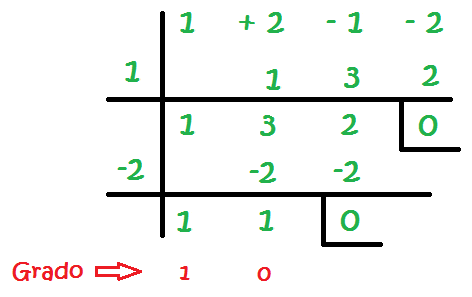
→ TEOREMA DEL RESTO
P(x) : Q(x)
P(x)= x4 − 3x2 +2 Q(x)= x − 3
P(3) = 3*4 − 3*3*2 + 2 = 12 − 18 + 2 = -4
3. ECUACIONES
→PRIMER GRADO
Definición: Una ecuación de primer grado es una igualdad de dos expresiones en las que aparece una incógnita cuyo valor está relacionado a través de operaciones aritméticas. Se denominan ecuaciones de primer grado si el exponente de la incógnita es uno.
Ejemplo:

→PRIMER GRADO
Definición: Una ecuación de primer grado es una igualdad de dos expresiones en las que aparece una incógnita cuyo valor está relacionado a través de operaciones aritméticas. Se denominan ecuaciones de primer grado si el exponente de la incógnita es uno.
Ejemplo:
→ SEGUNDO GRADO
Definición: Una ecuación de segundo grado es una ecuación de tipo ax + bx + c = 0 e la cual a, b, c, son constante y a = 0, en otras palabras es toda ecuación en la cual el mayor exponente es 2.
→ BICUADRADAS
Definición: Las ecuaciones bicuadradas son ecuaciones de cuarto grado sin términos de grado impar
Ejemplo:

→ RACIONALES
Definición: Las ecuaciones racionales son ecuaciones en las que aparecen fracciones polinómicas.
Ejemplos:
→IRRACIONALES
Definición: Se llama ecuación irracional aquella que contiene una incógnita (o bien una expresión algebraica racional de la incógnita) bajo el signo radical.
Ejemplo:
4. SISTEMAS
Problema muy frecuente de sistemas:
5. INECUACIONES
Definición: Una inecuación es una desigualdad algebraica en la que sus dos miembros aparecen ligados por uno de estos signos:
< menor que 6x − 1 < 7
≤ menor o igual que 3x − 1 ≤ 7
> mayor que 5x − 1 > 7
≥ mayor o igual que 2x − 1 ≥ 7
> mayor que 5x − 1 > 7
≥ mayor o igual que 2x − 1 ≥ 7
Ejemplo:
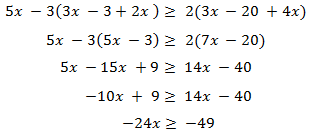
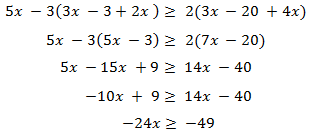
PARÁBOLAS
Bueno, aquí tienen mi parábola con la imagen de un nadador. He querido dibujar las parábolas en ambas manos y en la barbilla.
DEFINICIÓN DE PARÁBOLA: Una parábola es es el espacio geométrico de los puntos de un plano que tienen equidistancia respecto a un punto fijo y una recta.
Para añadir la parábola a mi imagen, tuve que tener en cuenta varias cosas que nuestra seño nos había explicado en un tutorial.
1. Hay dos tipos de curvas: convexa y cóncava.
➜ Si queremos que sea convexa; es decir, la curva estaría para arriba; tendremos que añadir el signo negativo antes de la parábola madre o la parábola que queramos hacer.
➜ Si queremos que sea cóncava; es decir, la curva estaría para arriba; tendremos que añadir el signo positivo antes de la parábola madre o la parábola que queramos hacer.
2. Si queremos desplazar la parábola hacia los lados, tenemos que tener en cuenta:
➜ Si queremos inclinar hacia la derecha (lado positivo) tenemos que poner el coeficiente negativo. Ejemplo (x-1)
➜ Si queremos inclinar hacia la izquierda (lado negativo) tenemos que poner el coeficiente positivo. Ejemplo (x+1)
3. Si queremos diseñar la apertura de la parábola, tendremos que tener en cuenta:
➜ Si queremos abrir la parábola, tenemos que multiplicarlo por un número que esté entre 0 y 1
➜ En el caso contrario, si queremos cerrar la parábola, tenemos que multiplicarlo por un número mayor que 1.
RETO DE LAS BOTELLAS
Bueno, aquí estamos otra vez, y esta vez para comentarles sobre el
reto de las botellas (también conocido como 'Water bottle flip'. Este
tema está arrasando por casi todo el mundo y nuestra clase ha decidido
investigar sobre el tema. Espero que les guste nuestras conclusiones.
¿QUÉ HACER PARA QUE MI BOTELLA CAIGA DE PIE?
Antes que nada, tendremos que tener en cuenta unas fases:
- Exploración (cuál es el problema, qué es lo que tenemos que averiguar...)
- Diseño
- Desarrollo (materiales y variables que debemos de tener en cuenta)
- Análisis y reflexión (obtendremos los aciertos y fallos y sacaremos conclusiones)
- Difusión (enseñarles nuestros resultados y comentárselos a nuestros compañeros)
- Evaluación
VARIABLES QUE DEBEMOS TENER EN CUENTA
- Constancia
- Fuerza e impulso
- Altura de la base
- Cantidad del líquido
- Ángulo
- Forma y tamaño de la botella
- Distancia de donde se tira
- Base de la botella (intentar que no se escache mucho)
¿CÓMO NOS ORGANIZAMOS?
Como
ya he dicho antes, hemos tenido que tener en cuenta algunas variables.
Y, sin duda alguna, no deberías cambiar las variables.
Bien,
para empezar fuimos a una sala (algo pequeña) pero lo suficientemente
espaciosa para que pudiésemos ir al grano. Nos hemos colocado a una
distancia de un metro de la mesa y nos hemos sentado en una silla.
También, nos pusimos de acuerdo en hacer 30 intentos por cada persona de
1/2, 1/3, 1/4 y 2/3. Para calibrar las botellas, las hemos pesado con
la gramera.
CONCLUSIONES
La conclusión a la que hemos llegado, es que con 1/4 es el mejor que se nos daba.
Ha
sido con la botella de 'Fuente Umbrella'. Ahora les pondré una gráfica
con los porcentajes de nuestro grupo para que veáis la gran diferencia.
GRÁFICAS CON NUESTROS RESULTADOS
ÁLGEBRA
Bueno, hoy día 22 de enero de 2017, pondré de nuevo en marcha mi blog. Hacía tiempo que no escribía, a causa de las vacaciones. Pero hoy nos pondremos las pilas, nada más y nada menos, que con álgebra. Les explicaré la factorización de polinomios (Ruffini) y también les pondré algunos vídeos para que repasen el tema de las ecuaciones de 1ª y 2ª grado, ya que tendría que estar más o menos controlado. Ahí vamos:
FACTORIZACIÓN DE POLINOMIOS (RUFFINI O TEOREMA DE FACTOR)
REGLA DE RUFFINI:
Para explicar los pasos a aplicar en la regla de Ruffini vamos a tomar de ejemplo la división:
(x4 − 3x2 + 2 ) : (x − 3)
1) Si el polinomio no es completo, lo completamos añadiendo los términos que faltan con ceros.
2) Colocamos los coeficientes del dividendo en una línea.
3) Abajo a la izquierda colocamos el opuesto del término independendiente del divisor.
4) Trazamos una raya y bajamos el primer coeficiente.
5) Multiplicamos ese coeficiente por el divisor y lo colocamos debajo del siguiente término.
6) Sumamos los coeficientes.
7) El número que finalmente obtenemos es el 56, lo que sería el resto.
NOTA: El cociente es un polinomio de grado inferior en una unidad al dividendo y cuyos coeficientes son los que hemos obtenido.
x^3 + 3x^2 + 6x + 18
TEOREMA DE FACTOR
El resto de la división del polinomio p(x) entre el binomio x-a es el valor numérico del polinomio en x=a, es decir p(a)
EJEMPLO:
(x4 − 3x^2 + 2) : (x − 3)
P(3) = 3x4 − 3 x 3^2 + 2 = 81 − 27 + 2 = 56
SIN EMBARGO, PODEMOS COMPROBAR LA SOLUCIÓN EFECTUANDO LA DIVISIÓN POR LA REGLA DE RUFFINI (EXPLICADA ANTERIORMENTE)
Efectivamente, está bien factorizada.
Después
de toda esta teoría (que espero que les haya sido muy útil), les pondré
los vídeos que estaban esperando desde el principio. Este tema la
verdad que ami, personalmente, me cuesta mucho ya que tengo que tener en
cuenta variedad de cosas. Aún así, estoy segura de que con práctica,
finalmente terminas cogiendole el truco y te resultará fácil. Espero que
ustedes también lo practiquen mucho.
VÍDEOS:
PRIMER GRADO
SEGUNDO GRADO
FACTORIZACIÓN DE POLINOMIOS
LOS INTERVALOS
Se llama intervalo al conjunto de números reales comprendidos entre otros dos dados: a y b que se llaman extremos del intervalo.
INTERVALO ABIERTO
Intervalo abierto, (a, b), es el conjunto de todos los números reales mayores que a y menores que b.
(a, b) = (a < x < b)
INTERVALO CERRADO
Intervalo cerrado, [a, b], es el conjunto de todos los números reales mayores o iguales que a y menores o iguales que b.
[a, b] ={a ≤ x ≤ b}
INTERVALO SEMIABIERTO A LA IZQUIERDA
Intervalo semiabierto por la izquierda, (a, b], es el conjunto de todos los números reales mayores que a y menores o iguales que b.
(a, b] = (a < x ≤ b}
INTERVALO SEMIABIERTO A LA DERECHA
Intervalo semiabierto por la derecha, [a, b), es el conjunto de todos los números reales mayores o iguales que a y menores que b.
[a, b) = [a ≤ x < b)
NOTA: CUANDO SE INCLUYE EL NÚMERO, SE PINTA EL CÍRCULO, CUANDO NO, NO.
RECOMENDACIÓN
Bueno, hoy no les voy a explicar teoría, pero escribo esta entrada para recomendarles dos vídeos que he estado viendo y me han servido muchísimo para entender mejor el tema. Espero que para ustedes también les sea útil. Aquí los tienen:
APROXIMACIONES
APROXIMACIONES: En el caso de estos números: pi, raíz cuadrada de 2, 5'675... 7'333... dificultan más el trabajo. Para ello, usamos valores próximos para simplificar los cálculos. Primero, les explicaré la teoría y luego pondré algunos ejemplos para que quede más claro. Existen tres formas para aproximarlos:
1. Aproximaciones por defecto:
Consiste en eliminar cifras a partir del orden considerado.
2. Aproximaciones por exceso: Se eliminan cifras a partir del orden considerado, pero se aumenta una unidad la última cifra que dejamos.
3. Redondeo (la más sencilla de todas):
Si el decimal último está comprendido entre 5 y 9, se aumenta una unidad.
Si está comprendido entre 1 y 5, se deja igual.
ERRORES: Cuando aproximamos un valor, cometemos un error por la pérdida de precisión con la que lo representamos.
Existen dos tipos de errores:
1. Error absoluto: Es el valor absoluto de la diferencia entre el valor real (vr) y el valor aproximado (va).
Fórmula: Ea= Vr - Va
2. Error relativo: Cociente entre el error relativo y valor real.
Fórmula: Er= Ea/ Vr
EJEMPLO: Error que cometemos al aproximar 1'25 a 1'2
Ea= Vr - Va
1'25- 1'20 = 0,05 (Ea)
Er= Ea/ Vr
0'05/ 1'25 = 0.04 (Er)
OJO: SI QUIERES APROXIMAR UN NÚMERO Y EL ÚLTIMO NÚMERO ES 5, SE AUMENTA.
PORCENTAJES
Bien, hoy día 26 de octubre de 2016, voy a escribirles sobre el tema de porcentajes.
CONCEPTOS:
Es una fracción cuyo denominador es 100.
Por ejemplo, 12 de 100 es 12/100
El porcentaje indica siempre una parte sobre 100.
Por ejemplo, el 12% indica 12 de cada 100.
Como una fracción, también puede ser una operación.
Por ejemplo, 12/100 = 0,12
En resumen: 12% de 100 = 12/100 = 0,12
¿CÓMO SE CALCULAN LOS PORCENTAJES?
Por ejemplo, el 15% de 250. Hay tres maneras de calcularlos:
1.) Dividir 250 entre 100 y multiplicar por 15
15% de 250 = 250/100 * 15 = 2,5 · 15 = 37,5
2.) También podemos multiplicar 15 por 250 y después dividir entre 100
15% de 250 = 15 * 250/ 100 = 375/100 = 37,5
3.) Pero también podríamos dividir primero 15 entre 100 y después multiplicarlo por 250
15% de 250 = 15/100* 250 = 0,15 * 250 = 37,5
ESQUEMA QUE DEBERÍAS 'TATUARTE' EN LA CABEZA PARA ENTENDERLO MEJOR
Cantidad total inicial * Porcentaje (Factor) = Cantidad añadida o descontada
Total · Porcentaje (Factor) = Descuento
AUMENTOS Y DISMINUCIONES, ¿CÓMO CALCULARLOS?
AUMENTOS:
Ej: Un reloj de 50 € aumenta su precio un 16 %. ¿Cuánto vale ahora?
Aumento = 50 € * 0.16 = 8€
Precio final = 50 € +8 € = 58€
En resumen, sería saber cuál es la cantidad que aumenta, y después de saberlo aumentarselo al precio inicial.
DISMINUCIONES:
Ej: Una nevera valía 620 €. Se rebaja un 40 %. ¿Cuánto vale ahora?
Disminución: = 620 € * 0.40 =248€
Precio final = 620 € - 248 € = 372 €
En resumen, sería saber cuál es la cantidad que disminuye, y luego quitárselo al precio inicial.
SI ES UN AUMENTO, TIENES QUE SUMARLE Y SI ES UNA DISMINUCIÓN, TIENES QUE RESTARLE
¿CÓMO CALCULAR LA CANTIDAD INICIAL CONOCIENDO LA VARIACIÓN DEL PORCENTAJE Y LA CANTIDAD FINAL?
Ej: Tras aumentar su precio un 35 %, un ordenador cuesta 783 €. ¿Cuánto valía antes de la salida?
Precio inicial * 1,35 = 783
Precio inicial = 783/ 1.35 = 580 €
Para hacer este tipo de problemas, tienes que fijarte en la siguiente fórmula:
Precio inicial * aumento o disminución del porcentaje = precio final
Espero que esta entrada les haya hecho mucho efecto, y que lo hayan entendido de maravilla. Nos vemos pronto ;)
LOS NÚMEROS
En este curso, vamos a estudiar los números reales, ya que los complejos se estudian en bachillerato.
Bien, para empezar, les voy a poner un esquema sobre todos los tipos de números que hay:
RACIONALES:
- Enteros: pueden ser positivos o negativos. Ej: 1,2,34,-5,-76...
- Decimales exactos: 0,25; 0,69; 1,2; 87,9
- Decimales periódicos puros: 0,666... 2,111... 6,545454...
- Decimales periódicos mixtos: 1,256666...
Voy a continuar diciéndoles el consejo que nos dió la seño para saber si un nº es exacto, periódico puro o periódico mixto:
Si es un número exacto, tendrá que ser múltiplo de 2 o de 5. Ej: 25, 30, 42, 60...
Si es un número periódico puro, tendrá que ser una potencia de 3. Ej: 9, 27, 181...
IRRACIONALES:
A pesar de que no vayamos a estudiar este tipo de números, les voy a dar algún ejemplo de tipos de irracionales que hay. Ej:
nº pi
nº e
Algunas raíces cuadradas, como de 3 o 99
Aunque no sea una profesional explicandolo, espero que lo hayan entendido estupendamente ;)
TRIGONOMETRIA
Lo que he aprendido de matemáticas hasta ahora, día 9 de Octubre de 2016, ha sido en relación con el tema de trigonometria.
1. Hay dos reglas fundamentales que son:
a)Si los triángulos rectangulos son semejantes, el cociente del c.o / hip , c.a /hip o c.o/ adj son iguales.
b) A medida que aumenta el angulo, disminuye el cociente del c.a/ hip, y sin embargo, el cociente de c.o/hip aumenta
2. Seno = c.o/ h
coseno= c.a/h
tangente= c.o/c.a
cosecante = h/c.o
secante= h/c.a
cotangente=c.a./c.o
3. Hay tres tipos de grados:
a) Sexagesimales (90·)
b)Centesimales (100·)
c)Radianes (pi/2)
4. Los datos minimos que me deberia dar un problema:
a)Un angulo y una medida de sus lados
b) Dos medidas de sus lados
5.TEOREMA FUNDAMENTAL
SEN2 a + COS2 a= 1

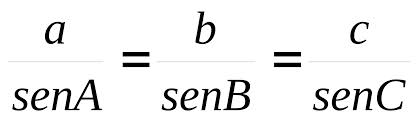








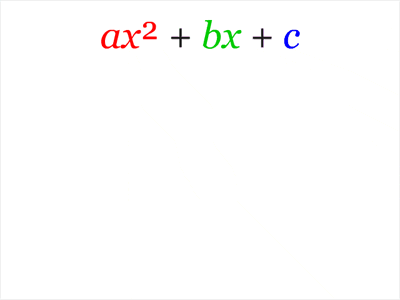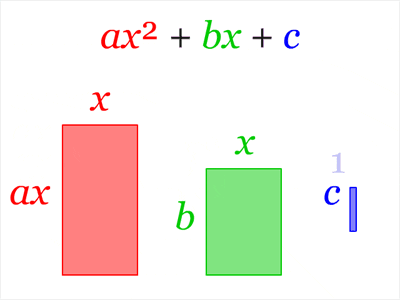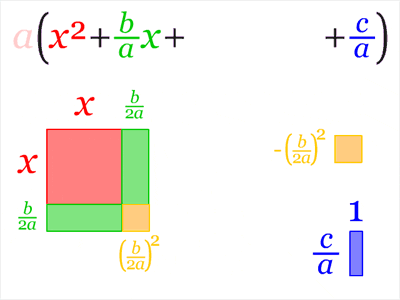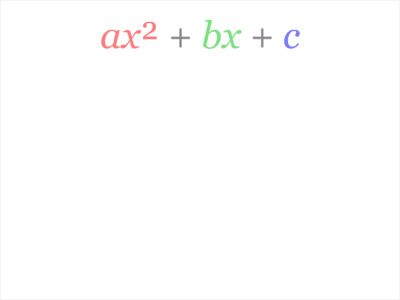
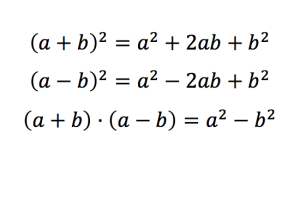





.png)
Tienes un blog muy trabajado y que me gusta mucho! Me encanta leer tus entradas.
ResponderEliminar